#Binary Search #Silver # Python
문제 요약
상근이는 나무 M미터가 필요하다. 상근이는 새로 구입한 목재절단기를 이용해서 나무를 구할것이다.
상근이는 절단기에 높이 H를 지정한다. 높이가 H보다 큰 나무는 H 위의 부분이 잘릴 것이고, 낮은 나무는 잘리지 않을 것이다.
이때, 적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오.
<제한 조건>
- 나무의 수 N, 상근이가 집으로 가져가려고 하는 나무의 길이 M은 (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000)
- 나무의 높이의 합은 항상 M보다 크거나 같기 때문에, 상근이는 집에 필요한 나무를 항상 가져갈 수 있다.
- 나무의 높이는 1,000,000,000보다 작거나 같은 양의 정수 또는 0이다.
문제 접근
이진 탐색의 변형 같은 문제이다. 이진 탐색의 대상과 이진 탐색의 성공 여부를 판단하는 지표가 다르다.
- 이진 탐색 대상이자 구하려는 값: 조건을 만족하는 절단기의 높이의 최댓값
- 지표: 상근이가 가져갈 수 있는 나무의 길이
left는 0 (절단기의 높이가 0일 때로, 모든 나무의 전체 길이를 베는 상황)
right는 max(trees) (절단기의 높이가 가장 긴 나무의 높이일 때로, 아무 나무도 베지 않는 상황)
으로 설정하고 while 문을 돌면서 이분 탐색을 진행하면 된다.
이때 pc = (left + right) // 2 가 조건을 만족하는지 확인하는 방법은
절단기 높이가 pc일 때 잘리는 나무 높이의 합을 구해서 그것을 M과 비교하는 것이다.
어려웠던 점
풀이 2개 중에 하나는 직관적으로 이해됐고, 다른 하나는 이해가 잘 안 됐다.
# 1. 이해가 잘 되는 풀이
import sys
def find_height(trees, M):
left = 0
right = max(trees) - 1
result = 0
while left <= right:
temp_sum = 0
pc = (left + right) // 2
for tree in trees:
if tree > pc:
temp_sum += (tree - pc)
if temp_sum == M:
return pc
elif temp_sum < M:
right = pc - 1
else:
result = pc
left = pc + 1
return result
if __name__ == '__main__':
N, M = map(int, sys.stdin.readline().split())
trees = list(map(int, sys.stdin.readline().split()))
print(find_height(trees, M))
이 풀이의 경우 절단기 높이가 pc일 때 잘리는 나무의 높이의 합을 계산해서 그것이 M과 같으면 pc를 반환하고, 그 합이 M보다 작으면 절단기의 높이를 더 낮추는 쪽으로 탐색을 더 진행하고, 그 합이 M보다 크면 절단기의 높이를 더 높이는 쪽으로 탐색을 더 진행한다.
이때 중요한 것은 잘리는 나무 높이의 합이 M보다 큰 경우에는 그 합을 잠정적으로 정답으로 간주할 수 있다는 것이다. 그래서 else문에서 result에 pc를 저장해두고 있다.
# 2. 이해가 어려웠던 풀이
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
heights = list(map(int, input().split()))
def get_max(heights):
pl = 0
pr = max(heights)
while pl <= pr:
pc = (pl + pr) // 2
cut_sum = sum(h - pc for h in heights if h > pc)
if cut_sum >= m:
pl = pc + 1
else:
pr = pc - 1
return pr
print(get_max(heights))
이 풀이의 경우에는 잘리는 나무 높이의 합이 m과 같은 경우를 따로 분기 처리하지 않고 잘리는 나무 높이의 합이 m보다 큰 경우와 같은 분기에서 처리하고 있다.
이 풀이에서 이해가 어려웠던 부분은 return 값으로 pr을 설정하고 있다는 점이었다. 처음에 생각했을 때는 pl이 왼쪽에 있는 값이고 pr이 오른쪽에 있는 값이니까 pr보다는 pl이 답에 가깝다고 생각했었다.
그런데 이분 탐색이 종료되는 경우는 다음 두 가지가 있다.
1. 한 번도 pc의 오른쪽을 탐색해본 적 없이 pl = pr = pc = 시작했을 때의 pl 지점에서 탐색 종료
2. 한 번이라도 pc의 오른쪽을 탐색해본 적이 있고, pl = pr = pc가 된 이후에 pl > pr이 돼서 탐색 종료
1번의 경우에는 계속 왼쪽 반만 탐색을 하다가, 즉 pr = pc - 1을 하다가 끝나는 경우이다.
2번의 경우에는 한 번이라도 pc의 오른쪽을 탐색해본 적이 있다는 것인데 이 말은 즉 pc부터 왼쪽 부분은 모두 조건을 만족하는 영역이라는 것이다. pc의 오른쪽을 탐색하는 것은 절단기 높이의 최댓값을 찾기 위해 pc의 오른쪽에도 혹시 조건을 만족하는 지점이 더 있는지 확인하는 것이다.
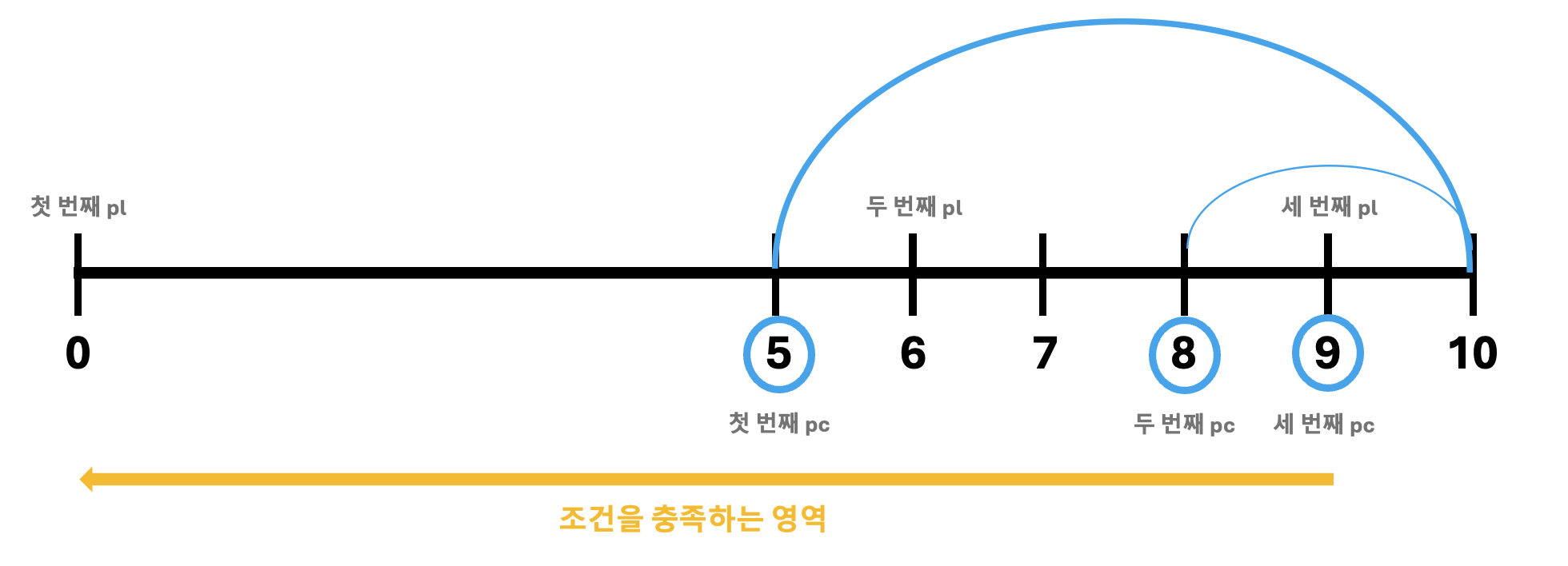
그러니까 pl > pr이 되기 전 pl = pr = pc 상황이 됐을 때 왼쪽(pl의 왼쪽)은 모두 조건을 만족하는 영역이다. 오른쪽은 조건을 만족하지 않는 영역이다. 그래서 항상 왼쪽 영역을 선택하는 pr = pc - 1을 리턴값으로 삼는 것이다.
소감
이분 탐색이 종료되는 순간이 어떤 상황인지를 잘 이해해야 한다는 걸 느끼게 해 준 문제였다.
'Data Structure & Algorithm' 카테고리의 다른 글
| [BOJ] 2470 두 용액 (0) | 2025.01.06 |
|---|---|
| [BOJ] 2110번 공유기 설치 (0) | 2025.01.05 |
| LeetCode 1582. Special Positions in a Binary Matrix (1) | 2024.10.29 |
| [이론] 자료 구조: 힙 heap (0) | 2024.08.18 |
| [이론] 완전 탐색 Brute force (0) | 2024.08.15 |